Дисперсионный анализ.

Понятие, назначение дисперсионного анализа. Виды дисперсионного анализа.

Дисперсионный анализ – анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.

(В зарубежной литературе именуется ANOVA – «Analisis of Variance»)

Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:

- Вариативность, обусловленную действием каждой из исследуемых независимых переменных.

- Вариативность, обусловленную взаимодействием исследуемых независмых переменных.

- Вариативность случайную, обусловленную всеми неучтенными обстоятельствами.

Вариативность, обусловленная действием исследуемых переменных и их взаимодействием соотносится со случайной вариативностью. Показателем этого соотношения является F – критерий Фишера (метод, не имеющий ничего общего, кроме автора, с «угловым преобразованием Фишера»).

F_эмпА = Вариативность, обусловленная действием переменной А / Случайная вариативность

F_эмпБ = Вариативность, обусловленная действием переменной Б / Случайная вариативность

F_эмпАБ = Вариативность, обусловленная взаимодействием А и Б / Случайная вариативность

В формулу расчета критерия F взодят оценки дисперсий, и, следовательно, этот метод относится к разряду параметрических. Чем в большей степени вариативность признака обусловлена исследуемыми переменными или их взаимодействием, тем выше эмпирические значения критерия F.

В отличие от корреляционного анализа, в дисперсионном исследователь исходит из предположения, что одни переменные выступают как влияющие (именуемые факторами или независимыми переменными), а другие (результативные признаки или зависимые переменные) – подвержены влиянию этих факторов. Хотя такое допущение и лежит в основе математических процедур расчета, оно, однако, требует осторожности рассуждений об источнике и объекте влияния.

Например, если мы выдвигаем гипотезу о зависимости успешности работы должностного лица от фактора Н (социальной смелости по Кэттелу), то не исключено обратное: социальная смелость респондента как раз и может возникнуть (усилиться) вследствие успешности его работы – это с одной стороны. С другой: следует отдать себе отчет в том, как именно измерялась «успешность»? Если за ее основу взяты были не объективные характеристики (модные нынче «объемы продаж» и проч.), а экспертные оценки сослуживцев, то имеется вероятность того, что «успешность» может быть подменена поведенческими или личностными характеристиками (волевыми, коммуникативными, внешними проявлениями агрессивности etc.)

Представим смысл дисперсионного анализа графически.

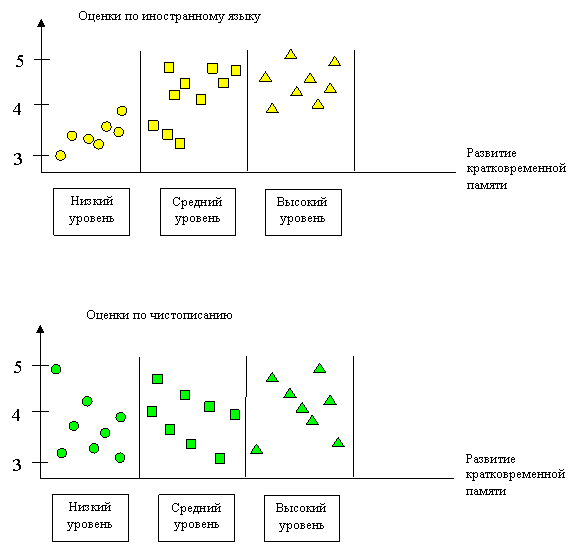
В примере, взятом из (1), иллюстрируется исследование зависимости учебной успеваемости школьников от развития кратковременной памяти. В качестве фактора рассматривался уровень развития кратковременной памяти, а в качестве результативных признаков – успеваемость по предмету. Видно, например, что фактор, по-видимому, оказывает существенное влияние при обучении иностранному языку, и незначим для чистописания, что, впрочем, вполне согласуется со здравым смыслом.

Приведенный пример обращает внимание также и на то, какими именно должны быть факторы?

Здесь фактор имел градации, то есть его величина изменялась при переходе от одной градации к другой. Следует знать, что такое условие отнюдь не обязательно: фактор может иметь градации, никак не связанные между собой количественным отношением, и может быть представлен хоть в номинальной шкале. В общем (и это точнее) говорят не о градациях фактора, а о различных условиях его действия. Возможность количественной градации фактора, таким образом, лишь частный случай.

В качестве иллюстрации этого положения скажем, что если отыщется исследователь, желающий определить зависимость яйценоскости от цвета курицы, то ничто не помешает ему применить дисперсионный анализ, и в качестве условий действия фактора «цвет» избрать, скажем, черных, белых и пестрых кур.

Формулировка гипотез в дисперсионном анализе.

Нулевая гипотеза:

«Средние величины результативного признака во всех условиях действия фактора (или градациях фактора) одинаковы».

Альтернативная гипотеза:

«Средние величины результативного признака в разных условиях действия фактора различны».

Виды дисперсионного анализа.

Дисперсионный анализ схематически можно подразделить на несколько категорий. Это деление осуществляется, смотря по тому, сколько, во-первых, факторов принимает участие в рассмотрении, во-вторых, - сколько переменных подвержены действию факторов, и, в-третьих, - по тому, как соотносятся друг с другом выборки значений.

При наличии одного фактора, влияние которого исследуется, дисперсионный анализ именуется однофакторным, и распадается на две разновидности:

- Анализ несвязанных (то есть – различных) выборок. Например, одна группа респондентов решает задачу в условиях тишины, вторая – в шумной комнате. (В этом случае, к слову, нулевая гипотеза звучала бы так: «среднее время решения задач такого-то типа будет одинаково в тишине и в шумном помещении», то есть не зависит от фактора шума.)

- Анализ связанных выборок. То есть: двух замеров, проведенных на одной и той же группе респондентов в разных условиях. Тот же пример: в первый раз задача решалась в тишине, второй – сходная задача – в условиях шумовых помех. (На практике к подобным опытам следует подходить с осторожностью, поскольку в действие может вступить неучтенный фактор «научаемость», влияние которого исследователь рискует приписать изменению условий, а именно, - шуму.)

В случае, если исследуется одновременное воздействие двух или более факторов, мы имеем дело с многофакторным дисперсионным анализом, который также можно подразделить по типу выборки.

Если же воздействию факторов подвержено несколько переменных, - речь идет о многомерном анализе.

Ограничения дисперсионного анализа и подготовка данных.

Дисперсионный анализ следует применять тогда, когда известно (установлено), что распределение результативного признака является нормальным.

Для проверки следует провести расчеты ассимметрии и эксцесса по следующим формулам:

A = Σ (xi – xср)³ / ns³

mA= √6/n

E = (Σ (xi – xср)⁴ / ns⁴ ) - 3

mE= 2√6/n ,

где А и Е – ассимметрия и эксцесс, а m_A и m_E – их ошибки репрезентативности. После подстановки значений не должно оказаться так, чтобы ассимметрия и эксцесс превышали более, чем втрое свои ошибки репрезентативности. При соблюдении этого требования, распределение можно считать нормальным.

Будем называть данные, относящиеся к одному условию действия фактора (к одной градации) дисперсионным комплексом.

Дисперсионный анализ требует также, чтобы между комплексами соблюдалось равенство дисперсий. В литературе по этому вопросу предлагается (и доказана правомочность предложения) удовлетворять такое требование уравниванием числа значений в каждом из комплексов. Иными словами, если в тихой аудитории решали задачу 10 человек, то и в шумную мы должны посадить столько же; если белых кур набралось 100, черных – 80, а пестрых – 70, - мы обязаны взять только по 70 кур каждого цвета. Причем, отбор следует осуществлять случайным образом.

(В SPSS эта возможность представлена так: Данные – Выбор регистров – Случайный образец регистров (радиокнопка) – Образец… (кнопка)).

. . .

Однофакторный дисперсионный анализ для несвязанных выборок.

Назначение метода.

Метод однофакторного дисперсионного анализа применяется в тех случаях, когда исследуются изменения результативного признака (зависимой переменной) под влиянием изменяющихся условий или градаций какого-либо фактора.

Влиянию каждой из градаций фактора подвержены разные выборки.

Должно быть не менее трех градаций фактора и не менее двух наблюдений в каждой градации.

Описание метода.

Расчеты начинаются с расстановки всех данных по столбцам, относящимся к каждому из факторов соответственно.

Следующим действием будет нахождение сумм значений по столбцам (то есть – градациям) и возведение их в квадрат.

Фактически метод состоит в сопоставлении каждой из полученных и возведенных в квадрат сумм с суммой квадратов всех значений, полученных во всем эксперименте.

Графическое представление метода.

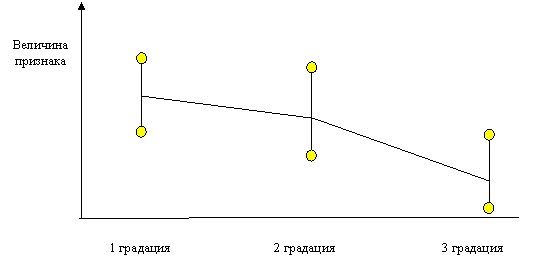
На рисунке схематически представлены три градации какого-либо фактора. Дисперсионный анализ позволяет определить, что преобладает: влияние фактора или случайная вариативность внутри групп (тенденция, выраженная кривой или размах отрезков, ограниченных кружками)?

Алгоритм расчета.

Промежуточные величины.

Tc	суммы индивидуальных значений по каждому из условий
Σ(T^2c)	сумма квадратов суммарных значений по каждому из условий
с	количество условий (градаций фактора)
n	количество значений в каждом комплексе (испытуемых в каждой группе)
N	общее количество индивидуальных значений
(Σxi)^2	квадрат общей суммы индивидуальных значений
Σ(xi)^2/ N	константа, необходимая для вычитания из каждой суммы квадратов
xi	каждое индивидуальное значение
Σ(xi)^2	сумма квадратов индивидуальных значений

Принятые в литературе сокращения:

СК или SS – сумма квадратов

SSфакт. – вариативность, обусловленная действием исследуемого фактора

SSобщ. – общая вариативность

SSсл. – случайная вариативность

MS – «средний квадрат» (математическое ожидание суммы квадратов, усредненная величина соответствующих SS)

df – число степеней свободы.

Основные вычисления.

Подсчитать SSфакт.	SSфакт. = 1/n ΣT^2c – 1/n (Σxi)^2
Подсчитать SSобщ.	SSобщ. = Σx^2i – 1/N (Σxi)^2
Подсчитать случайную остаточную величину SSсл.	SSсл. = SSобщ. – SSфакт.
Определить число степеней свободы	dfфакт. = с – 1 dfобщ. = N – 1 dfсл. = dfобщ. – dfфакт.
Разделить каждую SS на соответствующее число степеней свободы	MSфакт. = SSфакт. / dfфакт. MS сл. = SS сл. / df сл.
Подсчитать значение Fэмп.	Fэмп. = MSфакт. / MS сл.
Определить по таблицам критические значения F и сопоставить с ним полученное эмпирическое значение	При Fэмп. >= Fкр. H0 отклоняется.

. . .

Однофакторный дисперсионный анализ для связанных выборок.

Назначение метода.

Метод применяется в тех случаях, когда исследуется влияние разных условий действия фактора (градаций фактора) на одну и ту же выборку. (Одни и те же респонденты в разных условиях.)

Условий (градаций) должно быть не менее трех.

Индивидуальных значений по каждому условию должно быть не менее двух.

Описание метода.

В этом случае различия могут быть вызваны не только влиянием фактора, но и индивидуальными различиями между испытуемыми. При анализе несвязанных выборок это обстоятельство не оказывало воздействия за счет того, что выборки были различны, и сводилось к случайным причинам различий, - здесь же индивидуальные различия между элементами выборки (респондентами) необходимо особо учитывать. (Индивидуальные различия могут оказаться более значимыми, чем изменение условий действия фактора.) Исходя из сказанного, в расчеты вводятся дополнительные компоненты – суммы квадратов сумм индивидуальных значений.

Графическое представление.

Рисунок иллюстрирует пример решения анаграмм различной длины одними и теми же респондентами. Исследователей интересовало влияние длины анаграммы на время ее решения. (Выяснилось, что наибольшие трудности, что видно из диапазона времени, затраченного на решение, и его среднего значения, вызвала анаграмма из пяти букв.)

Расчет промежуточных величин.

Tc	Суммы индивидуальных значений по каждому из условий
ΣT^2c	Сумма квадратов суммарных значений по каждому из условий
с	Количество значений у каждого респондента, то есть – количество условий
n	Количество респондентов
N	общее количество значений
Tn	Суммы индивидуальных значений по каждому респонденту
ΣT^2n	Сумма квадратов сумм индивидуальных значений по респондентам
xi	каждое индивидуальное значение
(Σxi)^2	квадрат общей суммы индивидуальных значений
1/N(Σxi)^2	константа, необходимая для вычитания из каждой суммы квадратов
Σ(xi)^2	сумма квадратов индивидуальных значений

Основные вычисления.

Подсчитать SSфакт.	SSфакт. = 1/n ΣT^2c – 1/n (Σxi)^2
Подсчитать SSресп.	SSресп. =1/c ΣT^2n – 1/N (Σxi)^2
Подсчитать SSобщ.	SSобщ. = Σx^2i – 1/N (Σxi)^2
Подсчитать случайную остаточную величину SSсл.	SSсл. = SSобщ. – SSфакт. – SSресп.
Определить число степеней свободы	dfфакт. = с – 1 dfресп. = n – 1 dfобщ. = N – 1 dfсл. = dfобщ. – dfфакт. – dfресп.
Разделить каждую SS на соответствующее число степеней свободы	MSфакт. = SSфакт. / dfфакт. MS респ. = SS респ. / df респ. MS сл. = SS сл. / df сл.
Подсчитать значения F	Fфакт.= MSфакт. / MS сл. Fресп.= MSресп. / MS сл.
Определить по таблицам критические значения F и сопоставить с ними полученные эмпирические значения	При Fэмп. >= Fкр. H0 отклоняется.

Дисперсионный анализ в SPSS.

Для произведения расчетов воспользуемся гипотетическим примером о выяснении зависимости яйценоскости кур от их цвета.

Создадим две переменные, первая из которых будет содержать «данные» о снесенных курицей яйцах, вторая – сведения о ее цвете. Причем, первая переменная будет типа «Scale», а вторая (фактор цвета) – «Nominal», так как ни один из цветов не может быть «больше» других количественно.

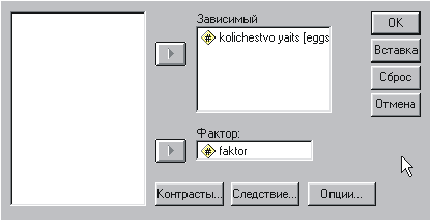
Далее следует выбрать:

Анализ – Средства сравнения – Односторонний анализ вариантов

(Analize – Compare means – One-Way ANOVA)

Появится окно, показанное на рисунке:

После нажатия кнопки «Следствие» появится возможность назначить дополнительную процедуру, позволяющую определить, какие именно подгруппы наиболее однородны, с указанием значимости, - то есть степени возможного доверия к этой информации. Для выбора этой возможности следует пометить флажком окошко критерия Дункана.

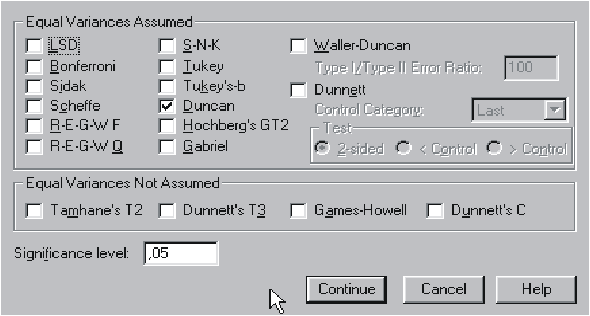
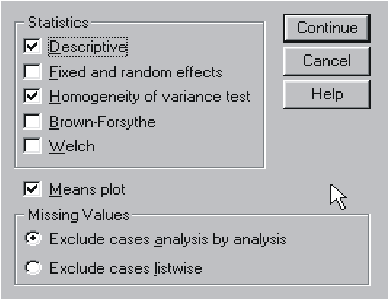
Нажав кнопку «Опции», получаем возможность:

- заказать вывод описательных статистик, что поспособствует увеличению наглядности;

- произвести расчет однородности дисперсий;

- получить в файле вывода график средних значений по градациям фактора.

Для этого необходимо пометить флажками соответствующие окошки:

____________________________________________________________

После получения файла вывода будем располагать следующей информацией:

Oneway (Однофакторный анализ)

Descriptives (описательные статистики) kolichestvo yaits
	N	Mean	Std. Deviation	Std. Error	95% Confidence Interval for Mean		Minimum	Maximum
					Lower Bound	Upper Bound
belaya kurica	20	6,15	1,424	,319	5,48	6,82	3	8
chernaya kurica	20	3,90	1,165	,261	3,35	4,45	2	6
pestraya kurica	20	9,45	11,024	2,465	4,29	14,61	5	56
Total	60	6,50	6,746	,871	4,76	8,24	2	56

Test of Homogeneity of Variances (Проверка однородности дисперсий) kolichestvo yaits
Levene Statistic	df1	df2	Sig.
2,625	2	57	,081

ANOVA (Дисперсионный анализ по Фишеру) kolichestvo yaits
	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	311,700	2	155,850	3,743	,030
Within Groups	2373,300	57	41,637
Total	2685,000	59

Post Hoc Tests (Апостериорные вычисления)

Homogeneous Subsets (Однородность подгрупп)

kolichestvo yaits Duncan
	N	Subset for alpha = .05
FAKTOR		1	2
chernaya kurica	20	3,90
belaya kurica	20	6,15	6,15
pestraya kurica	20		9,45
Sig.		,275	,111
Means for groups in homogeneous subsets are displayed.
a Uses Harmonic Mean Sample Size = 20,000.

Means Plots

Первой в очереди будет таблица, содержащая описательные статистики, то есть сведения:

- об объеме выборки,

- среднем значении,

- стандартном отклонении,

- стандартной ошибке,

- нижней и верхней границе доверительного интервала,

- минимальном значении,

- максимальном значении.

Следующей идет таблица, информирующая о результатах проверки на однородность дисперсий по критерию Левена, с указанием степени значимости (Sig. – от significance – значимость).

Далее следует основная таблица с расчетами критерия F Фишера, включающая промежуточные сведения о сумме квадратов, степени свободы, среднем квадрате, собственно значении критерия F, и значимости различий.

Вслед за этой, идет таблица апостериорной проверки по методу Дункана, которая сообщает о возможности деления выборки на однородные подгруппы с указанием значимости. В рамках нашего примера это означает, что черные и белые куры могут составить одну подгруппу, причем мера доверия к такому способу группировки выражается числом 0,275. Белые и пестрые же могут объединиться в один «клуб», сообразно с числом 0,111. То есть эта таблица показывает возможность группировки кур по сходной яйценоскости и достоверность (правомочность) такого действия.

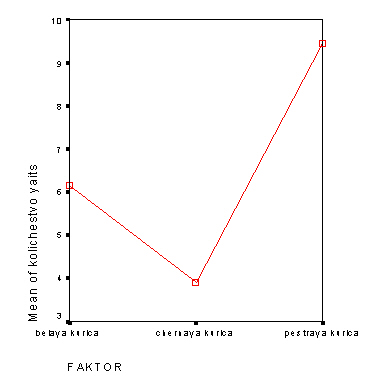
В заключение будет представлен график (строго говоря: линейчатая гистограмма) зависимости средней яйценоскости (У) от цвета курицы (Х).

Дополнительная информамция.

Следует отметить, что в нашем примере не было получено значимых различий между цветами кур. (Мы помним, что данные вымышленные!) С целью проверки, мы удвоили количество кур, сохраняя им прежнее соотношение яйценоскости (то есть выделили все значения, скопировали и продублировали, прибавив к низу соответствующих столбцов), а после – утроили. Результаты расчетов в обоих этих случаях приводятся ниже для того, чтобы дать возможность наблюдать изменения результатов расчетов при увеличении объема выборки и сохранении прежних соотношений яйценоскости. Следует обратить внимание на:

- тенденцию к большей значимости различий по критерию F,

- возможность более достоверно разделить выборку на подгруппы по методу Дункана.

Удвоенный объем выборки

Oneway

Descriptives kolichestvo yaits
	N	Mean	Std. Deviation	Std. Error	95% Confidence Interval for Mean		Minimum	Maximum
					Lower Bound	Upper Bound
belaya kurica	40	6,15	1,406	,222	5,70	6,60	3	8
chernaya kurica	40	3,90	1,150	,182	3,53	4,27	2	6
pestraya kurica	40	9,45	10,882	1,721	5,97	12,93	5	56
Total	120	6,50	6,718	,613	5,29	7,71	2	56

Test of Homogeneity of Variances kolichestvo yaits
Levene Statistic	df1	df2	Sig.
5,388	2	117	,006

ANOVA kolichestvo yaits
	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	623,400	2	311,700	7,683	,001
Within Groups	4746,600	117	40,569
Total	5370,000	119

Post Hoc Tests

Homogeneous Subsets

kolichestvo yaits Duncan
	N	Subset for alpha = .05
FAKTOR		1	2
chernaya kurica	40	3,90
belaya kurica	40	6,15
pestraya kurica	40		9,45
Sig.		,117	1,000
Means for groups in homogeneous subsets are displayed.
a Uses Harmonic Mean Sample Size = 40,000.

Утроенный объем выборки

Oneway

Descriptives kolichestvo yaits
	N	Mean	Std. Deviation	Std. Error	95% Confidence Interval for Mean		Minimum	Maximum
					Lower Bound	Upper Bound
belaya kurica	60	6,15	1,400	,181	5,79	6,51	3	8
chernaya kurica	60	3,90	1,145	,148	3,60	4,20	2	6
pestraya kurica	60	9,45	10,835	1,399	6,65	12,25	5	56
Total	180	6,50	6,708	,500	5,51	7,49	2	56

Test of Homogeneity of Variances kolichestvo yaits
Levene Statistic	df1	df2	Sig.
8,151	2	177	,000

ANOVA kolichestvo yaits
	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	935,100	2	467,550	11,623	,000
Within Groups	7119,900	177	40,225
Total	8055,000	179

Post Hoc Tests

Homogeneous Subsets

kolichestvo yaits Duncan
	N	Subset for alpha = .05
FAKTOR		1	2
chernaya kurica	60	3,90
belaya kurica	60	6,15
pestraya kurica	60		9,45
Sig.